Question Solve the system using the substitution method x 2y = 6 3x 2y = 2 This is what I did 3x 2y = 2 x = 2y 3 _____ (2y 3) 2y = 6X=y3 x/3 y/2=6 Substituting in ( x/3y/2=6) =>Solve the following equations by substitution method 2x − 3y = −1 and y = x − 1 Solution Question 5 Solve the following equations by substitution method y = −3x 5 and 5x − 4y = −3 Solution Question 6 Solve the following equations by substitution method −3x − 3y = 3 and y = −5x − 17 Solution Question 7

How Do You Solve The System 4x 2y 6 And X Y 3 Socratic
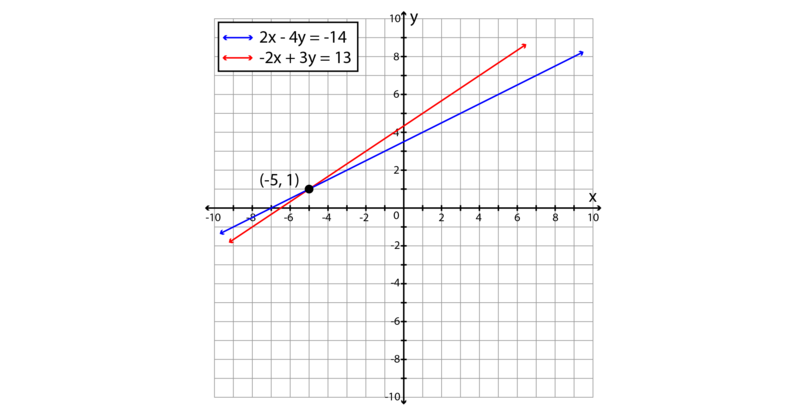
X-y=3 x/3 y/2=6 by substitution method
X-y=3 x/3 y/2=6 by substitution method-Answer (1 of 2) If x y = 4, Then y = 4 x if y = 4 x Then 2x (4 x) = 5 by substituting y's value in terms of x into the equation 2x (4 x) = 5 2x 4 x = 5 x = 3 If you use the first equation, x y = 4 Then substituting x gives you 3 y = 4 Which means y = 1 So x = 3 anTranscript Example 7 Solve the following pair of equations by substitution method 7x – 15y = 2 x 2y = 3 7x – 15y = 2 x 2y = 3 From (1) 7x – 15y = 2 7x = 2 15y x = (𝟐 𝟏𝟓𝒚)/𝟕 Substituting the value of x in (2) x 2y = 3 (2 15𝑦)/7 2𝑦=3 Multiplying both sides by 7 7 ×




3 Systems Of Linear Equations
X 3 y 2 = 13 6Steps for Using the Substitution Method in order to Solve Systems of Equations Solve 1 equation for 1 variable (Put in y = or x = form) Substitute this expression into the other equation and solve for the missing variable Substitute your answer intoLet's make x y = − 4 equation 1 y = − 3x 2 equation 2 The substitution method means that you will take an equation and plug it into another one to get rid of an unknown These questions may sometimes require you to rearrange one of the equations first, so that there is only one variable* on one side of the equation
Click here👆to get an answer to your question ️ Solve equations using substitution method x y = 3 and x y = 0 Join / Login >>Pair of Linear Equations in Two Variables Solve equations using substitution method x − y = 3 and x y = 0 A 2 3I will choose xTherefore equation 1 becomesx= 3y So by substitution method ,plug in 3y for x in equation 2 Therefore3x2y=3 will become 3(3y)2y = 3 93y2y=3 3y2y= 39 (by collecting like terms y = 6 To get our x valueWe have to substitute the value of y which is 6 in equation 1 (preferably) xy=3 Plug in (6) as y in this
X y = 4 where, x = 9, y = 5, (ii) s t = 3;Solve the Given equation in Elimination method and Substitution MethodX = 3 Place x = 3 back into either equation to fin



Cbse 10 Math Cbse Linear Equations In Two Variables Ncert Solutions




Rd Sharma Solutions For Class 10 Maths Chapter 3 Pair Of Linear Equations In Two Variables Updated For 21 22 Coolgyan Org
Solve the following pair of linear equations by the substitution method (3x)/2 (5y)/3 = 2, x/yy/2 = 13/6 MathematicsQUESTION 71 Use the substitution method to solve this system y 2 x 4 3 x y 9 from MGF MGF( at Full Sail University9x 3y = 9 where, x can have infinitely many solutions, (iv) 02x 03y = 13;



Pair Of Linear Equations In Two Variables




Ncert Solutions Class 10 Maths Chapter 3 Pair Of Linear Equations In Two Variables Ship Hang Nhanh
Systemofequationscalculator substitution method x2y=2x5, xy=3 en Related Symbolab blog posts High School Math Solutions – Systems of Equations Calculator, Nonlinear In a previous post, we learned about how to solve a system of linear equations In this2x = 6 ==>Solve the Following Pair of Linear (Simultaneous ) Equation Using Method of Elimination by Substitution 2( X 3 ) 3( Y 5 ) = 0 5( X 1 ) 4( Y 4 ) = 0 CISCE ICSE Class 9 Question Papers 10 Textbook Solutions Important Solutions 6 Question Bank Solutions 145 Concept Notes




Exercise 33 Solve The Followi See How To Solve It At Qanda




How Do You Solve The System 4x 2y 6 And X Y 3 Socratic
17) solve this linear system using the method of substitution 2yx=10 y= 3/2x1 ) simplify then solve by substitution 2(x4)y=6 3x2(y3)=13 just need help with these 2 You can view more similar questions or ask a new questionA 2 x b 2 y c 2 = 0 (2) Step I Find the value of one variable, say y, in terms of the other ie, x from any equation, say (1) Step II Substitute the value of y obtained in step 1 in the other equation ie, equation (2) This equation becomes equation in one variable x only Step III Solve the equation obtained in step II to getSubstitution Method – Example Study the example below that shows how to use the substitution method in systems of equations Example Solve for x and y if 3x 2y = 4 and x 4y = 3 Answer x = 1 and y = 1/2 Step 1 Label the equations Label the equations A and B (A) 3x 2y = 4 (B) x 4y = 3 Step 2 Isolate one of the variables



Mfm2p




Solve X Y 3 And X 3 Y 2 6 By Substituting Methos Scholr
Y = 3 2x 4x y 3 is not an equation, so let's assume you meant 4x y = 3 4x y = 3 ==>04 x 05 y = 23 (v) √ 2 x √ 3 y = 0;Transcript Ex 33, 1 Solve the following pair of linear equations by the substitution method (iii) 3x – y = 3 9x – 3y = 9 3x – y = 3 9x – 3y = 9 Solving (1) 3x – y = 3 3x = y 3 x = (𝒚 𝟑)/𝟑 Putting value of x in (2) 9x – 3y = 9 9((𝑦 3)/3)−3𝑦=9 3(y 3) – 3y = 9 3y 9 – 3y = 9 3y – 3y 9 = 9 0 9 = 9 9 = 9 The statement is true for all values of x So



Use The Substitution Method To Solve The System Of Gauthmath




In The Following System Of Equation Determine Whether The System Has A Unique Solution No Solution Or Infinitely Many Solution In Case There Is A Unique Solution Find It 2x 3y
Take that value of x, and substitute it into the first equation given above (x y = 3) With that substitution the first equation becomes (1y) y = 3 That means 1 2y = 3 Subtract 1 from each side 2y = 2 So y = 1 Substitute that value of y into either of the two original equations, and you'll get x = 2To solve a pair of equations using substitution, first solve one of the equations for one of the variables Then substitute the result for that variable in the other equation 2xy=6,2xy=2 2 x y = 6, 2 x − y = 2 Choose one of the equations and solve it for x by isolating xThis discussion on Solve using substitution method 3x/25y/3=2 , x/2 y/2=13/6?ans x=2,y=3?




Solve The Following Pairs Of Linear Equations By The Elimination Method And The Substitution Method Frac X 2 Frac 2y 3 1wedge X Frac Y 3 3 Snapsolve




Q 1 2x 5y Xy 6 4x 5y Xy 3 Solve By Substitution Method Q 2 X 3 Y 4 11 5x 6 Y 3 7 0 Solve By Substitution Answer Fast Plz Maths Pair Of Linear Equations In Two Variables
A system of equations consists of a set of two or more equations with the same variables In this section, we will study linear systems consisting of two linear equations each with two variables The system {2x − 3y = 0 − 4x 2y = − 8 { 2 x − 3 y = 0 − 4 x 2 y = − 8 is one such system A solution to a linear system, or04x 05 y = 23Answer Let's first solve for 'y' in the 1st equation, then substitute that into 2nd equation 2x y = 3 ==>




7 Y 3 2 X 2 14 4 Y 2 3 X 3 2 Youtube



Solving Systems Of Linear Equations
2 Substitution method xy=16 and y=3x 3 Solve the system by the substitution method y= 2x 7 and 2x 3y = 19 4 xy= 1 and xy= 5 Solve the system by the addition method 5 Solve the system by the addition method 4x13y= 8 and 2x13y=4 6 Solve the system by graphing 3x2y=12 and x 2y= 4;S/3 t/2 = 6 where, s = 9, t = 6, (iii) 3x y = 3;Solve by Substitution Calculator Step 1 Enter the system of equations you want to solve for by substitution The solve by substitution calculator allows to find the solution to a system of two or three equations in both a point form and an equation form of the answer Step 2 Click the blue arrow to submit




Solutions Section 2 6




Graph Graph Inequalities With Step By Step Math Problem Solver
Cancel the common factor Divide y y by 1 1 Divide 3 3 by 3 3 Replace all occurrences of y y with 1 1 in each equation Tap for more steps Replace all occurrences of y y in x = y x = y with 1 1 Remove parentheses The solution to the system is the((2 15𝑦)/7) 7×2𝑦=7×3 (2 15y) 14y = 21 15y 14y = 21 – 2 29y = 21 – 2Solution Solution provided by AtoZmathcom Substitution Method Solve Linear Equation in Two Variables Solve linear equation in two variables 1 12x 5y = 7 and 2x 3y 5 = 0 2 x y = 2 and 2x 3y = 4 3 7y 2x 11 = 0 and 3x y 5 = 0



Simultaneous Equations Graphically Solve Graphically The System Of Equations



The Substitution Method
Simplify each of the following 1 2 a 2 b 3 b a 2 Medium View solution >Explanation 2x 3y = 6 x y = 3 Let's solve for x in the second equation x = 3 −y Now let's plug (3 − y) in for x in the first equation 2(3 −y) 3y = 6 6 − 2y 3y = 6 y = 0NCERT Solutions for Class 10 Maths Chapter 3 Exercise 33 Question 1 Summary On solving the pair of linear equations by the substitution method we get the variables as (i) x y = 14;



Waynesville K12 Mo Us




Ncert Solutions For Class 9 Maths Chapter 4 Linear Equations In Two Variables
Are solved by group of students and teacher of Class 10, which is also the largest student community of Class 109 x − 3 y = 9 (iv) 02 x 03 y = 13;X − y = 4 (ii) s − t = 3;



Sfdr Cisd Org




Exercise 33 1 Solve The Follo See How To Solve It At Qanda
In substitution method, we first find the value of any one of the variables using anyone of the equations and then, substitute that value in another equation Followed by, we solve the equation so obtained to get the solution Now, lets put the value of y in equation (2) {we always try to choose the equation which is easier to solve} x = 2Free equations calculator solve linear, quadratic, polynomial, radical, exponential and logarithmic equations with all the steps Type in any equation to get the solution, steps and graphThe Questions and Answers of Solve these linear equations by substitution method 3x/2 5y/3 =2 x/3 y/2 =13/6?



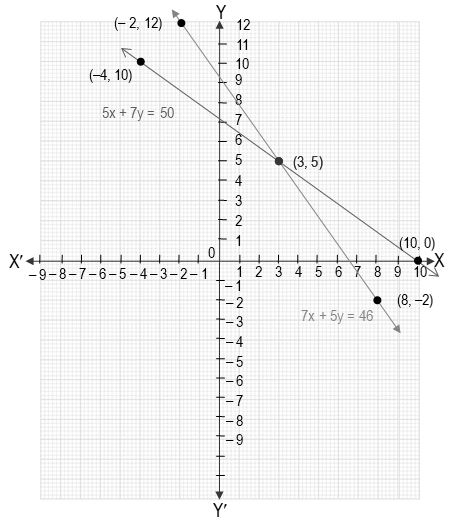
2x 3y 0 3x 4y 5




3 Systems Of Linear Equations
Math Algebra Algebra questions and answers = 3 (6 points) Solve the system of nonlinear equations (x2 x y = 7 by substitution methodHeya!!, it can be done with any method but the answer remains same i m doing with SUBSTITUTION method By substitution method xy=3=>Solve the following pairs of linear equations by the substitution method 02x 03y = 13, 04x 05y = 23 asked in Mathematics by Samantha ( 3k points) pair of linear equations in




7 Solve The System Of Equations Ii X 3 Y 2 X Y Homeworklib



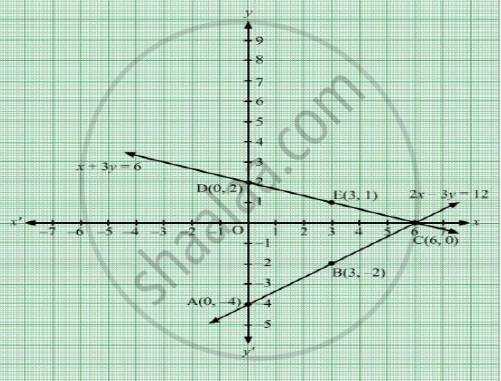
Solve The Following Simultaneous Equation Graphically 2x 3y 12 X Y 1 Algebra Shaalaa Com
Use the substitution method to solve the system of equations 2x 5y = 6 x y = 2 Equation 1 is in the correct ax by format Equation 2 is in the correct ax by format Rearrange Equation 2 to solve for x x y = 2 Add y to both sides to isolate x x y y = 2 y x = 2 y This is our Revised Equation 2S 3 t 2 = 6 (iii) 3 x − y = 3;Solve the following pair of linear equations by the substitution method 3 x − y = 3 9 x 2 x 4 y = 3;



Maths Guru Please Help Me Solve This Simultaneous Equations For My Young Photo Education 2 Nigeria




X Y 3 And X 3 Y 2 6 Solve The Following Pair Of Linear Equations By The Elimination Method And Brainly In
(x, y) = (35, 2) Apart from the stuff given above, if you need any other stuff in math, please use our google custom search here Solving linear equations using substitution method Solving linear equations using cross multiplication method Solving one step equationsSolve for x and y y = 3x 6 − 2x 4y = 4 y = 3x 6 − 2x 4y = 4 Choose an equation to use for the substitution The first equation tells you how to express y in terms of x, so it makes sense to substitute 3x 6 into the second equation for y − 2x 4 y = 4 − 2x 4 (3x 6) = 4 Substitute 3x 6 for y into the second3x/2 5y/3 = 2 and x/3y/2=13/6 Solve using substitution method



2x 3y 13 7x 2y



Systems Of Linear Equations
Solve the following pair of linear equations by the substitution method (i) x y = 14;4x (3 2x) = 3 ==>Solve each of the following systems of equations by the method of crossmultiplication (xy)/xy = 2, (x y)/xy = 6 asked Apr 27 in Linear Equations by Gargi01 ( 506k points) pair of linear equations in two variables



6 3 Substitution Method Simultaneous Linear Equations Siyavula




Exercise 33 Solve The Followi See How To Solve It At Qanda
Solve the following pair of linear equations by the substitution method (vi)`(3x)/2(5y)/3=2` , `x/3y/2=13/6` Updated On To keep watching this video solution for FREE, Download our AppQuestion 2 Substitution method xy=16 andSolve the following pair of linear equations by the substitution method `(3x)/(2)(5y)/(3)=2` `(x)/(3)(y)/(2)=(13)/(6)`



Solve 5 X 1 1 Y 2 2 And 6 X 1 3 Y 2 1 Studyrankersonline




Warm Up Solve Each Equation For X 1 Y X Y 3x 4 Ppt Video Online Download
1 Explain the advantages and disadvantages of both the substitution method and the elimination method for solving a system Help please The only reasons I can think of is because in substitution it might be more difficult cause algebra Solve the following system using the substitution method 6x 2y = 4 y = 3x 2Y=x6 3x2y=8 Using substitution method 3x2(x6)=8 3x2x12=8 5x= x=4 Now substitute x in one of the two equations given to find y y=46 y=2 The solution is (4,2)1 2 y 6 x = 6 Medium View solution >



Important Questions For Class 10 Maths Chapter 3 Pair Of Linear Equations In Two Variables Learn Cbse



Solved Find The Common Solution Of Each Using The Elimination Substitution And Graphical Method 2x Y 2 X 3y 36 2 3x Y 6 X Y 6 3 Course Hero
Click here 👆 to get an answer to your question ️ Solve {y=x−x3y=1 Use the substitution method (5, −3) (4, −4) (0, −8) (2, −6)√ 3 x − √ 8 y = 0 (vi) 3 x 2 − 5 y 3 = − 2;Is done on EduRev Study Group by Class 10 Students The Questions and Answers of Solve using substitution method 3x/25y/3=2




Let S Learn Solving Systems Using The Substitution Method




Systems Of Equations And Linear Equalities
Solve the following system of equations by substitution First, we will solve the first equation for y y Now we can substitute the expression x − 5 x − 5 for y y in the second equation Now, we substitute x = 8 x = 8 into the first equation and solve for y y Our solution is ( 8, 3) ( 8, 3) Check the solution by substituting ( 8, 3) ( 8When the greater of the two numbers increased by 1 divides the sum of the numbers, the result is 2 3




Selina Chapter 6 Linear Equations Including Problems Icse Solutions Class 9 Maths




Solved 6 2 Solving Systems Of Linear Equations 455 We Have Chegg Com



6 X Y 7 X Y 3 1 2 X Y 1 3 X Y




Solved Solve The Following Pair Of Linear Equations By The Substitution Method Begin Array Ll Text I X Y 14 Text Ii S T 3 X Y 4 Frac S 3 Frac T 2 6 End Array Begin Array Llll Text Iii 3




3 Systems Of Linear Equations




Ncert Class 10 Mathematics Chapter Wise Questions And Answers And Solutions




7x 3y 1 0




X 2 2y 3 1 And X Y 3 3 Solve By Elimination Method Brainly In




Solving Systems Of Equations With Fractions Or Decimals Video Lessons Examples And Solutions



How To Solve The Following Simultaneous Equations By Elimination Method A 2x 3y 12 X Y 1 B 3x Y 10 C X 3y 1 3x 2y 4 0 D 5 Quora




Chapter 5 Review Exercises




Systems Of Equations Substitution Method Ppt Video Online Download




Example 18 Solve 5 X 1 1 Y 2 2 6 X 1 3 Y 2 1 Examples




Solution Of X Y 3 And X 3 Y 2 6 By Elimination Method Brainly In




1 Topic The Substitution Method 2 Topic The Substitution Method California Standard 9 0 Students Solve A System Of Two Linear Equations Ppt Download




Ncert Class 10 Mathematics Chapter Wise Questions And Answers And Solutions



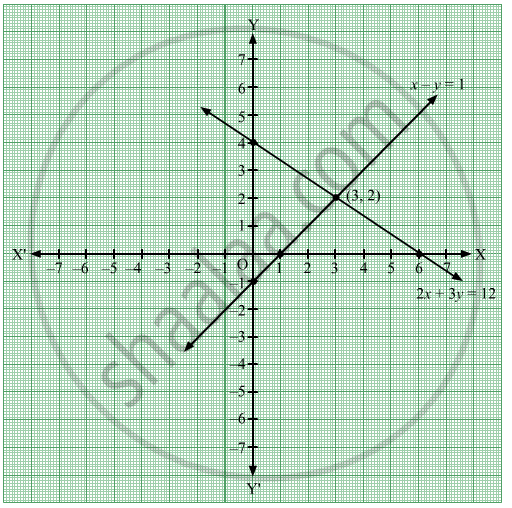
Solve Graphically The System Of Equations 2x 3y 12 X 3y 6 Find The Coordinates Of The Vertices Of The Triangle Formed By These Two Lines And The Y Axis Mathematics Shaalaa Com




Solve For X And Y X Y 3 4x 3y 26



Solve The Following Pairs Of Linear Equations By The Substitution Method 3x 2 5y 3 2 X 3 Y 2 13 6 Sarthaks Econnect Largest Online Education Community



Elimination




Solve The Following Pair Of Linear Equations By The Substitution Method I X Y 14 X Y 4 Ii S T 3 S 3 T 2 6 Iii 3x Y 3 9x 3y 9 Iv 0 2 X 0 3 Y 1 3 0 4 X 0 5 Y 2 3 V Sqrt 2 X Sqrt 3 Y 0 Sqrt 3 X Sqrt 8 Y 0 Vi 3x 2 5y 2 2 X 3 Y 2 13 6



What Are X And Y From The System Equation 2x 3y 4 X Y 6 Quora




Solve The Following System Of Equations 27 X Y 15 X Y 2 And 30 X Y 1 X Y 3 Mathematics Topperlearning Com X68shsoo




7 Solve The System Of Equations Ii X 3 Y 2 X Y Homeworklib




Cbse Ncert Solution For Class 10 Maths Linear Equations In 2 Variables
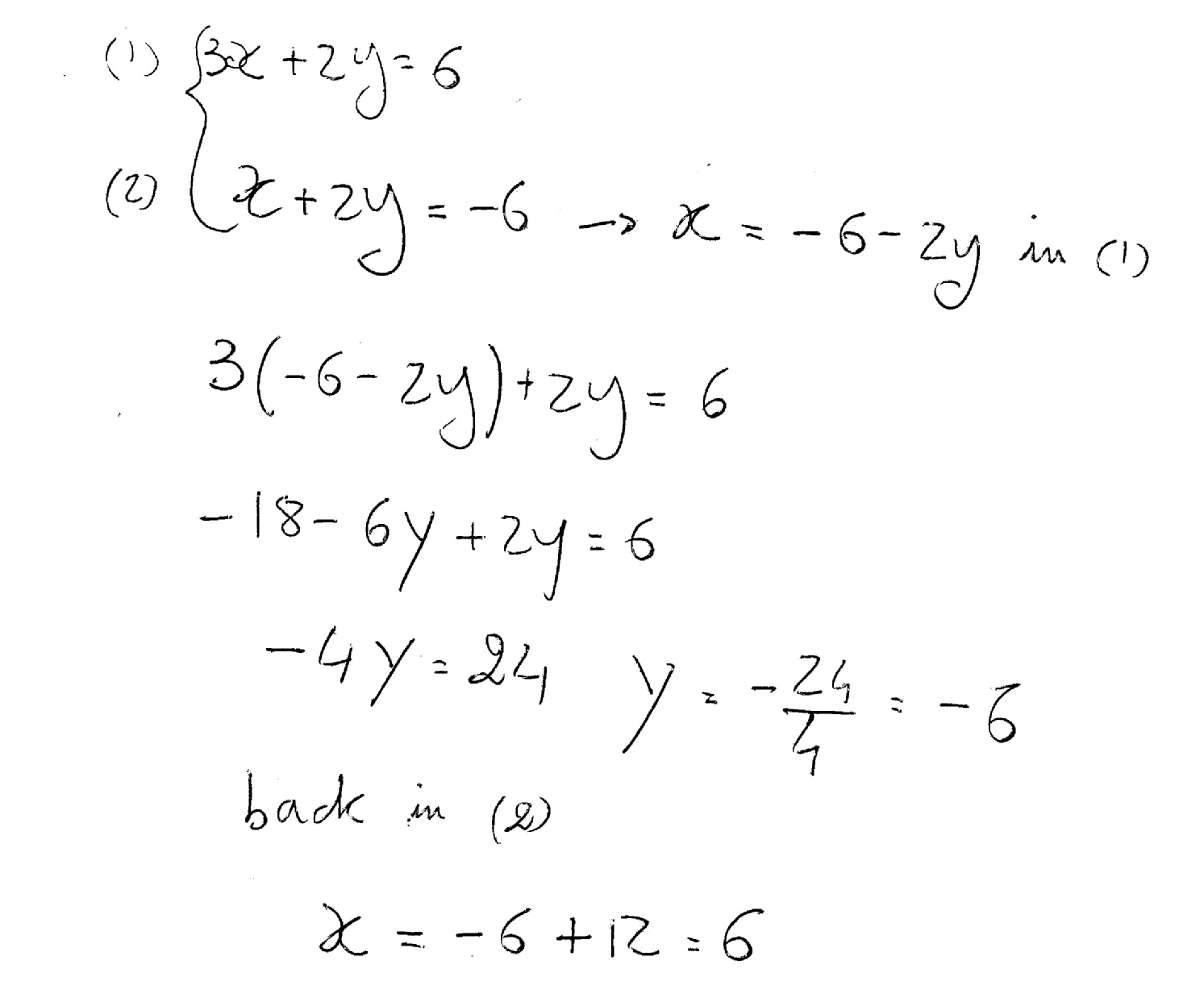



How Do You Solve By Substitution 3x 2y 6 And X 2y 6 Socratic




10 A 3 Mathematics Systems Of Linear Equations



Who Can Solve This X Y 15 And X Y 3 Find X And Y Quora




1 Solve The Following Pair Of Linear Equations By The Math



Using Matrix Method Solve The System Of Equations 3x 2y 2z 3 X 2y 3z 6 2x Y Z 2 Studyrankersonline




X Y 3 X 3 Y 2 6 Youtube




Ionic Transport Properties Of La X Y 3 X Fe 5 O 12 D Compounds A The Download Scientific Diagram



Pjiju6wqvb4tdm




Homework Pencil Red Pen Highlighter Notebook Calculator Answer




Ex 3 3 Q1 Solve The Following Pair Of Linear Equations By The Substitution Method I




Answered Y 4 3 1 2 12x 10y 4 3 5 2 Bartleby



Graph Graph Inequalities With Step By Step Math Problem Solver




X 2 2y 3 1 And X Y 3 3 Find X And Y Values Using Elimination And Substitution Method Youtube
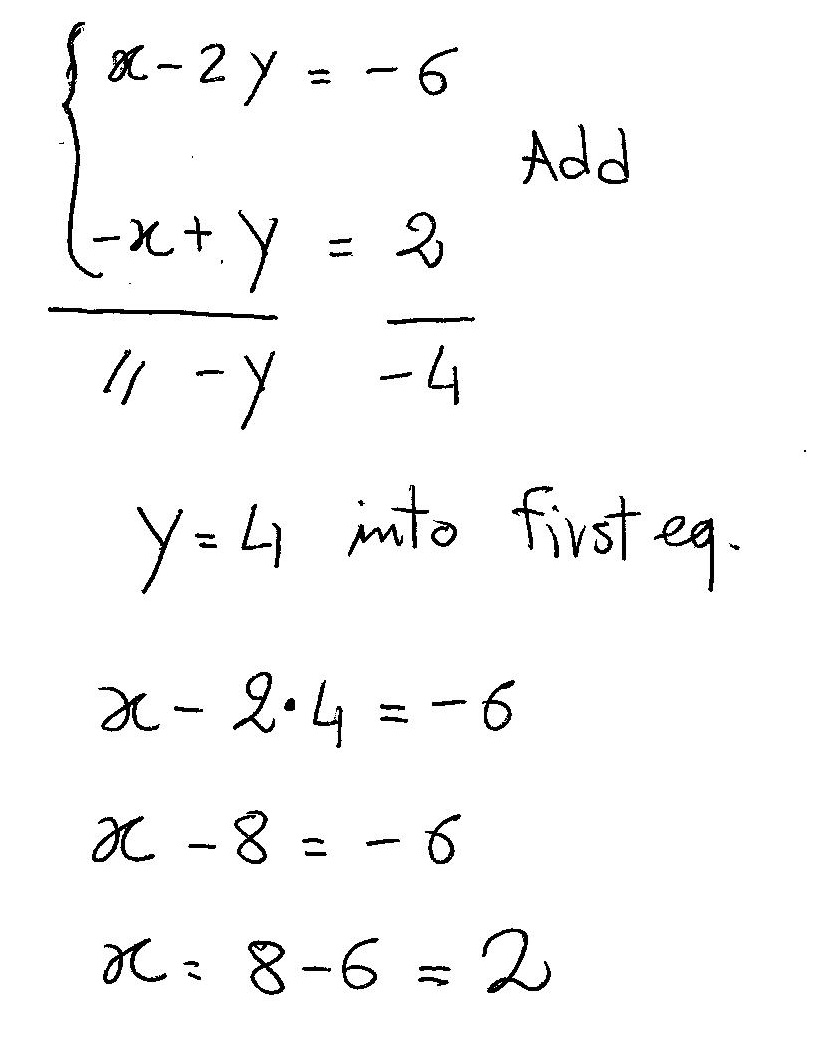



How Do You Solve X 2y 6 And X Y 2 Socratic




70以上 X5 Y5 Z5 ニスヌーピー 壁紙



Solve The Following Pairs Of Linear Equations By The Substitution Method 3x 2 5y 3 2 X 3 Y 2 13 6 Sarthaks Econnect Largest Online Education Community
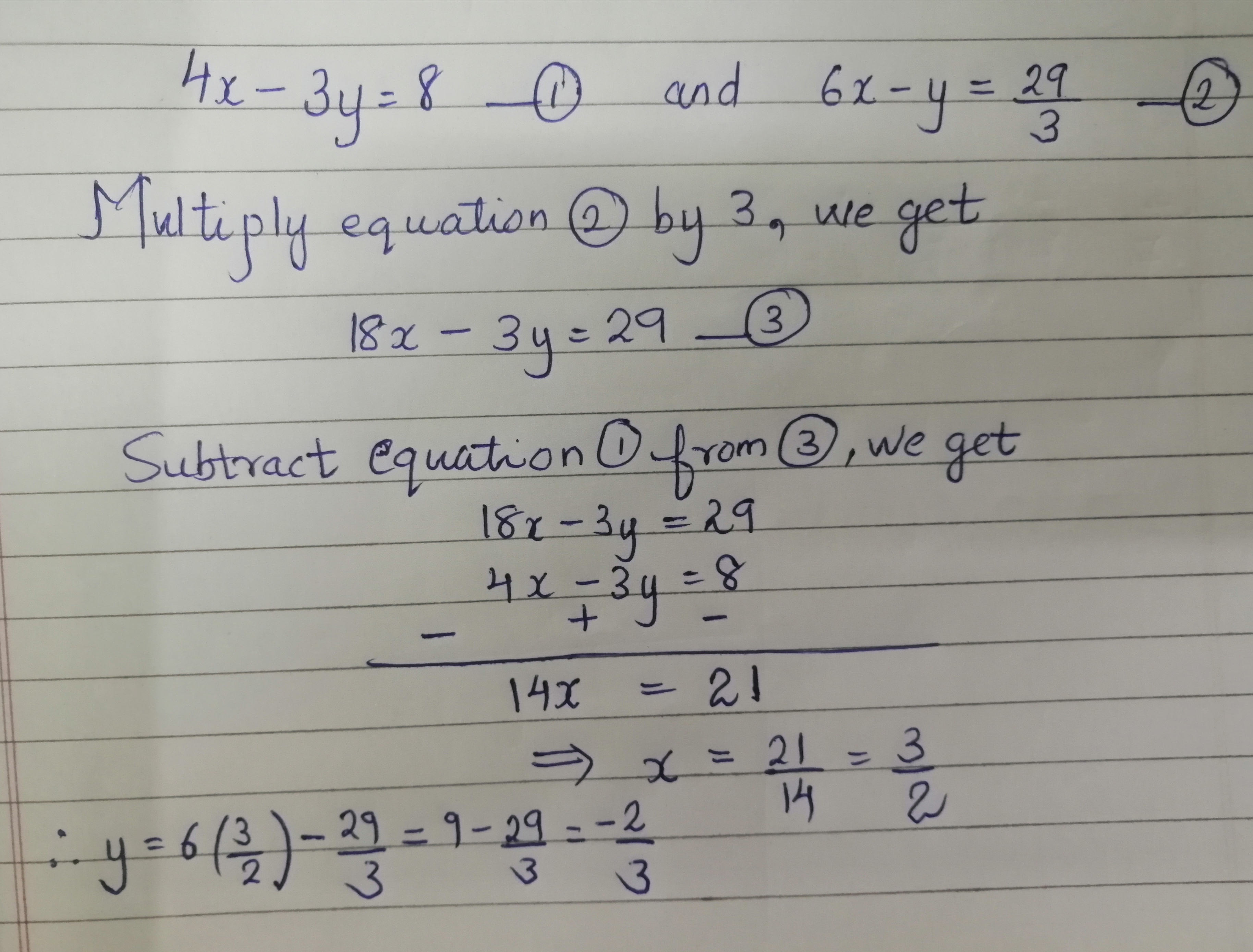



Solve The Sum 4 X Minus 3 Y Is Equal To 8 And 6 X Minus Y Is Equal To 29 Upon 3 By Elimination Of Y Only Mathematics Topperlearning Com 3c9x0inn




X 2 2y 3 1 Amp X Y 3 3 Solve By Eliminations Or Substitution Method Brainly In




Y Xy 3 1 X 2 1 2 Y 0 1 Harushley



X 3 Y 3



The Substitution Method



6 3 Substitution Method Simultaneous Linear Equations Siyavula




Solved 4 Given F X And G X Find F G X 5 8 X Chegg Com



Simultaneous Equation Question The Student Room



Solve The Following Systems Of Equations 6 X Y 7 X Y 3 1 2 X Y 1 A X Y Where X Y 0 And X Y 0 Sarthaks Econnect Largest Online Education Community




Solved Solve Each System Using The Substitution Method Egin Array L Y X 2 6 X 9 X Y 3 End Array
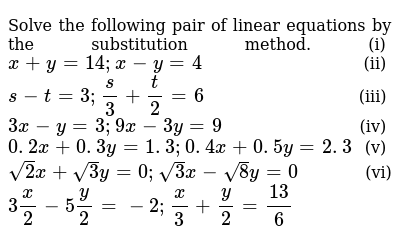



Solve The Following Pair Of Linear Equations By The Substitution Method I X Y 14 X Y 4 Ii S T 3 S 3 T 2 6 Iii 3x Y 3 9x 3y 9 Iv 0 2 X 0 3 Y 1 3 0 4 X 0 5 Y 2 3 V Sqrt 2 X Sqrt 3 Y 0 Sqrt 3 X Sqrt 8 Y 0 Vi 3x 2 5y 2 2 X 3 Y 2 13 6




Ppt Chapter 3 Systems Of Linear Equations Powerpoint Presentation Free Download Id 114




印刷 X Y5 2x 3y5 ニスヌーピー 壁紙




J19




Ex 3 3 1 I Solve By Substitution X Y 14 X Y 4 Video



Cbse 10 Math Cbse Linear Equations In Two Variables Ncert Solutions



Solving Linear Systems




1 Solve The Following Pair Of Linear Equations By The Substitution Method 1 X Y 14 Ii S T 3 S 6 X Y 4 Ii 3x Y 3 9x 3y 9 3 2 Iv 0 2x 0 3y 1 3 0 4x




Solve For X And Y 40 X Y 2 X Y 5 And 25 X Y 3 X Y 1 Mathematics Topperlearning Com Idbi1itt



Simultaneous Equations Gmat Math Study Guide




Ex 3 6 1 Iii Iv 4 X 3y 14 3 X 4y 23 Ex 3 6




Find The Value Of X And Y X 3 Y 4 11 5x 6 Y 3 7 By Substitution Method Maths Meritnation Com



Acpsd Net




Systems Of Equations With Substitution 2y X 7 X Y 4 Video Khan Academy




Ex 3 4 1 I Class 10 Solve By Elimination And Substitution



0 件のコメント:
コメントを投稿