In elementary algebra, completing the square is a technique for converting a quadratic polynomial of the form a x 2 b x c {\displaystyle ax^{2}bxc} to the form a 2 k {\displaystyle a^{2}k} for some values of h and k Completing the square is used in solving quadratic equations, deriving the quadratic formula, graphing quadratic functions, evaluating integrals in calculus, such asThen compare the vertex equation \( m = a (x – h)^2 K \) , the vertex of parabola is \( h = – b / 2a and k = c – b^2 / 4a \) However, an Online Slope Calculator helps to find the slope (m) or gradient between two points in the Cartesian coordinate plane How to Convert vertex form to standard form Write the function in the form f(x)=a(xh)^{2}k by completing the square Then identify the vertex q(x)=2 x^{2}12 x11
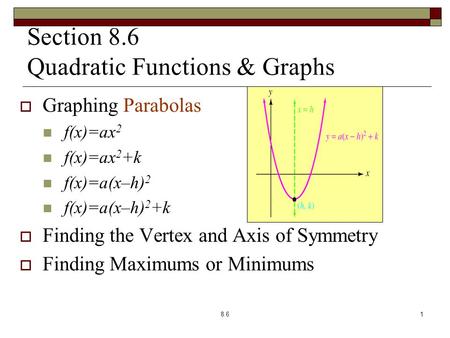
Transformations Review Vertex Form Y A X H 2 K The Vertex Form Of A Quadratic Equation Allows You To Immediately Identify The Vertex Of A Parabola Ppt Download
F(x)=a(x-h)^2 k how to find a
F(x)=a(x-h)^2 k how to find a-Use binomial theorem ( a b) 2 = a 2 2 a b b 2 to expand ( 3 x 1) 2 hfx=9x^ {2}6x13 h f x = 9 x 2 6 x 1 3 Add 1 and 3 to get 4 Add 1 and 3 to get 4 hfx=9x^ {2}6x4 h f x = 9 x 2 6 x 4 The equation is in standard form The equation is in standard form f '( − 1) = Δy Δx = 2 1 = 2 And g'( − 1) = Δy Δx = 4 3 We can conclude h'( − 1) = 2 ⋅ ( − 4 3) 4 3( −2) = − 16 3 The other exercise, to find k'( −1), follows a very similar approach, i will leave it for you, feel free to ask if anything is unclear Answer link



Www Scasd Org Cms Lib Pa Centricity Domain 1229 2 2 a2 17 unit 2 2 ws packet lg Pdf
1 You found h ( 2) Instead we want to find h ′ ( 2) First, take the derivative of h ( x) = f ( x) g ( x) with respect to x and use the given values above to find h ′ ( 2) So h ′ ( x) = f ′ ( x) g ′ ( x) and we will let x = 2 to obtain h ′ ( 2) = f ′ ( 2) g ′ ( 2) = 2 ( − 5) = − 3 Thus h ′ ( 2 Article Summary X To find the vertex of a quadratic equation, start by identifying the values of a, b, and c Then, use the vertex formula to figure out the xvalue of the vertex To do this, plug in the relevant values to find x, then substitute the values for a and b to get the xvalueExplore the parent graph y=x^3 Experiment with the values of a, h, and k What happens to the graph as these values change?
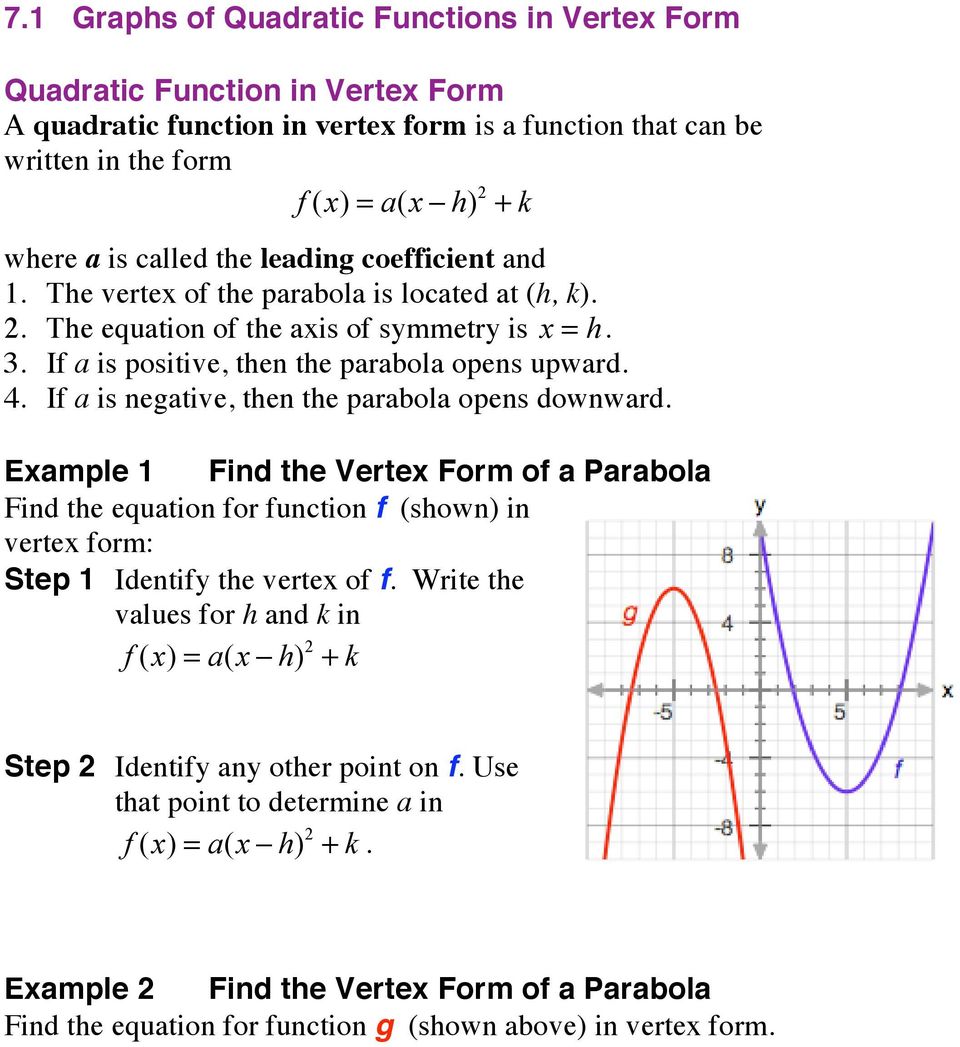
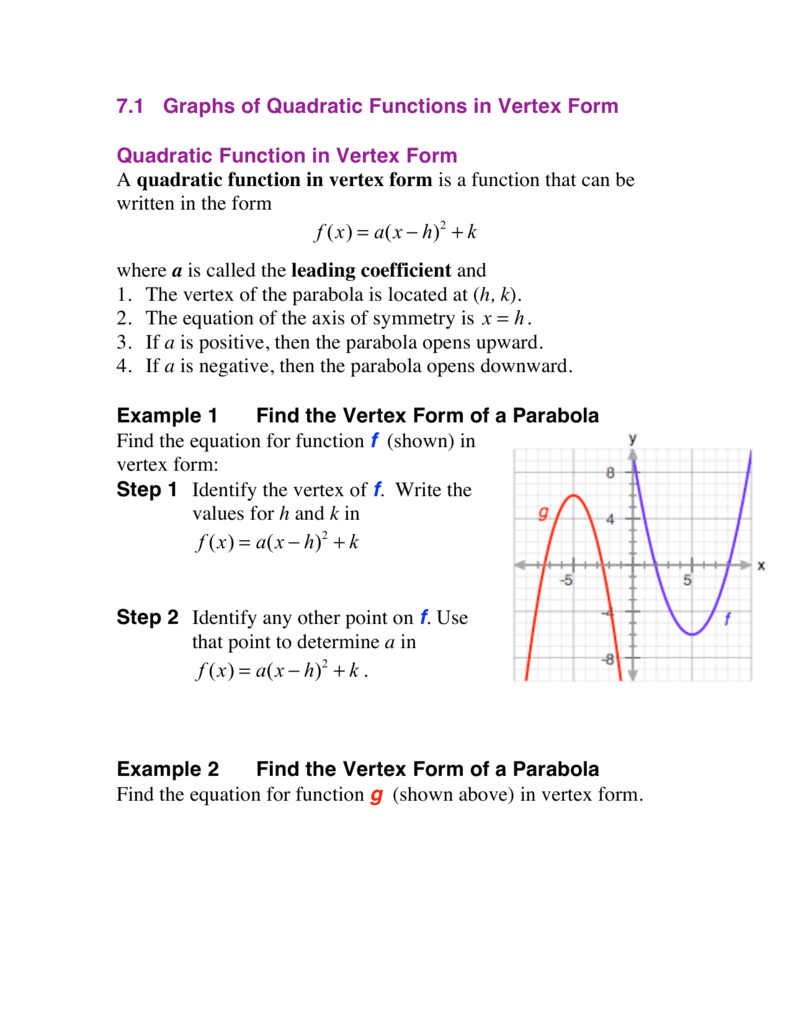
Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutorNEW Interested in Finding Out the Top "{{3}} Challenges that Can Get YOU in Trouble with Math"?Any quadratic function can be written in the standard form f (x) = a (x h) 2 k where h and k are given in terms of coefficients a , b and c Let us start with the quadratic function in general form and complete the square to rewrite it in standard form Given function f (x) f (x) = ax 2 bx c factor coefficient a out of the terms in x
Please Subscribe here, thank you!!!Just as y = mx b is a useful format for graphing linear functions, y = a(x h)^2 k is a useful format for graphing quadratic functions We will explore its uses and learn how to convert anyFree functions calculator explore function domain, range, intercepts, extreme points and asymptotes stepbystep



Graphing Quadratic Functions




Range Of Quadratic Functions Article Khan Academy
Vertex form is y=a(xh) 2 k The vertex of an equation in vertex form is (h,k) In vertex form, we have x MINUS h So if we're trying to just pick out 'h', we need to flip the sign that's in front of itH(x) = f (x)g (x) h ( x) = f ( x) g ( x) Since f (x)gx f ( x) g x is constant with respect to f f, the derivative of f (x)gx f ( x) g x with respect to f f is 0 0 0 0Y = a(x −h)4 k The turning point is at (h,k) When sketching quartic graphs of the form y = a(x − h)4 k, first identify the turning point To add further detail to the graph, the xaxis and yaxis intercepts are found Example 2 Sketch the graph of the function y = (x − 2)4 − 1 Cambridge University Press ¥ Uncorrected Sample Pages ¥



Www Hackensackschools Org Site Handlers Filedownload Ashx Moduleinstanceid 1615 Dataid Filename Vertex form transformations notes day 1 Pdf




Find The Vertex Of The Qudratic Function F X X 2 6x 42 Then Express The Qudrat Plainmath
To Convert from f (x) = ax2 bx c Form to Vertex Form Method 1 Completing the Square To convert a quadratic from y = ax2 bx c form to vertex form, y = a ( x h) 2 k, you use the process of completing the square Let's see an example Convert y = 2x2 4x 5 into vertex form, and state the vertex Equation in y = ax2 bx c formSimple and best practice solution for y=a(xh)2k equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, soComposition Functions Composition functions are functions that combine to make a new function We use the notation to denote a composition f g is the composition function that has f




Vertex Form In 5 Minutes What Is Vertex Form How Do I Find It Mike S Calculators With Steps Free 21




Quadratic Formula Calculator
The following applet allows you to select one of 4 parent functions The basic quadratic function f(x) = x^2 The basic cubic function f(x) = x^3 The basic absolute value function f(x) = x The basic square root function y = sqrt(x) In each of these functions, you will investigate what the parameters "a", "h", & "k" will do to the graph the parent function y = f(x) when we graph theF(x) = a(x h) 2 k The term (x h) 2 is a square, hence is either positive or equal to zero (x h) 2 ≥ 0 If you multiply both sides of the above inequality by coefficient a, there are two possibilities to consider, a is positive or a is negative case 1 a is positive a(x h) 2 ≥ 0 Add k to the left and right sides of the inequality a(x h) 2 k ≥ kThis video shows how to use horizontal and vertical shifts together to graph a radical function



Assignment 2 Investigating The Relationship Between The Two Standard Forms Of The Graph Of A Parabola




3 Ways To Find The Maximum Or Minimum Value Of A Quadratic Function Easily
Then type x=6 Try it now 2x3=15 @ x=6 Clickable Demo Try entering 2x3=15 @ x=6 into the text box After you enter the expression, Algebra Calculator will plug x=6 in for the equation 2x3=15 2(6)3 = 15 The calculator prints "True" to let you know that the answer isRead the book Dr Pan just finished!!Grab a copy here hQuestion This question is from textbook solving quadratic functions of the form f(x)=a(xh)2k(that 2 is a squared) i know how to get the value of a,h,k, but i dont know what they mean when they say choose some values for x in example 1 they have 7 values for x, but in example 2 they have 5 values for x so how do you know how many numbers to chose forthe value of x?




Quadratic Function Wikipedia
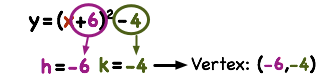



How Do You Convert A Quadratic From Standard Form To Vertex Form By Completing The Square Printable Summary Virtual Nerd
A quadratic function f in vertex form is written as f(x) = a(x h) 2 k where h and k are the x and y coordinates respectively of the vertex (minimum or maximum) point of the graph The graph of of f is a parabola with the vertical line x = h as an axis of symmetry Find quadratic function knowing its vertex and a point Example 1Graph of quadratic functions in vertex form g(x) = a(x h) 2 k A quadratic function in vertex form g(x) = a(x h) 2 k is the basic quadratic function f(x) = x 2 that has been transformed 1) From x 2 to (x h) 2 shift h units right if h is positive or h units left if h is negativeFor a function f (x), the difference quotient would be f(xh) f(x) / h, where h is the point difference and f(xh) f(x) is the function difference The difference quotient formula helps to determine the slope for the curved lines The f(xh) f(x) / h calculator can be used to find the slope value, when working with curved lines
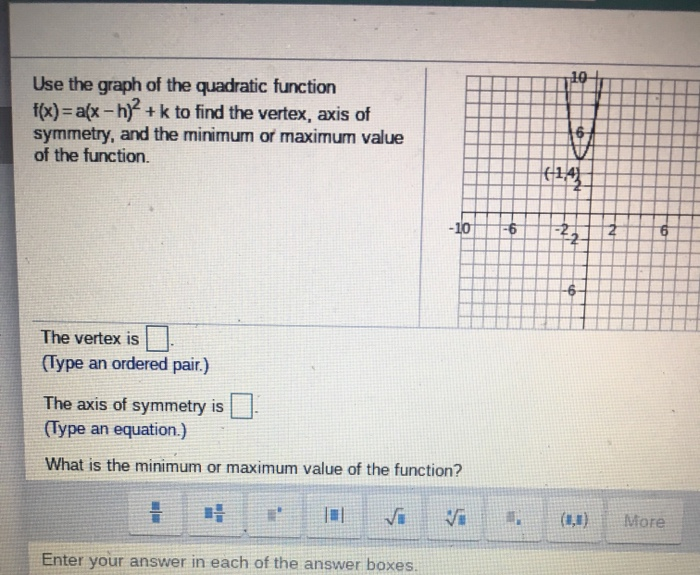



10 Use The Graph Of The Quadratic Function F X Chegg Com




Also Identify The Vertex No Need To Sketch Write The Quadratic Function In A X H 2 K Form Hint Homeworklib
Solution for Write the function in f(x) = a(x − h)2 k form Determine the vertex and the axis of symmetry of the graph of the function f(x) = 9x2 54x† x = a is a minimum if f0(a) = 0 and f00(a) > 0;Consider the graph of the parabola y=ax^2 Its vertex is clearly at (0,0) Now, if you replace x with xh in any equation, its graph gets shifted to the right by a distance of h
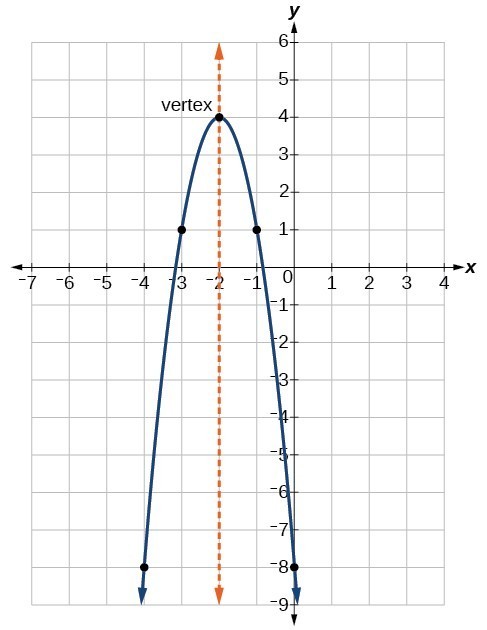



Understand How The Graph Of A Parabola Is Related To Its Quadratic Function College Algebra



Graph F X X H 2 K Youtube
color(red)( f(x) = (x1)^24) The vertex form of a quadratic is given by y = a(x – h)^2 k, where (h, k) is the vertex The "a" in the vertex form is the same "a" as in y = ax^2 bx c Your equation is f(x) = x^22x3 We convert to the "vertex form" by completing the square Step 1 Move the constant to the other side f(x)3 = x^22x Step 2Solution for f (x)=a (xh)2k equation Simplifying f (x) = a (x 1h) * 2 k Multiply f * x fx = a (x 1h) * 2 k Reorder the terms fx = a (1h x) * 2 k Reorder the terms for easier multiplication fx = 2a (1h x) k fx = (1h * 2a x * 2a) k fx = (2ah 2ax) k Solving fx = 2ah 2ax k Solving for variable 'f'Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange




Determine The Quadratic Function Of The Form F X Chegg Com



7 1 Graphs Of Quadratic Functions In Vertex Form Pdf Free Download
Substitute ah and a for x in the formula for f(x) and simplify to find (f(ah)f(a))/h = 2a 2 h >f(x) = x^22x3 Then (f(ah) f(a))/h =(((ah)^22(ah)3) (a^22a3))/h =(color(red)(cancel(color(black)(a^2)))2ahh^2color(blue)(cancel(color(black)(2a)))2hcolor(green)(cancel(color(black)(3)))color(red)(cancel(color(black)(a^2)))color(blue)(cancel(color(black)(2a)))color(green)(cancel(color(black)(3))))/h =2a2h So lim_(h>0) (f(ah) f(a))/h = lim_(h>0) (2a2h) = 2a2About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us CreatorsFree math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutor



Http Www Math Wsu Edu Faculty Dzhang 1fall14 1lecturenotes Fall14 Wed9 10 Pdf



Graph By Transformations F X A X H 2 K Youtube
Answer to 6 Let f(x,y) = (x y2, x3 5y), Xo = (1, 1) and h Who are the experts?Finally, to find the y intercept of an exponential in which h is not 0, just plug 0 as f(x)/y, and solve for x Exponential Equations To solve an exponential equation, you use logarithms (remember, logs and exponentials are inverses), specifically the power propertyFind f(xh)f(x)/h f(x)=x^23x7 Consider the difference quotient formula Find the components of the definition Tap for more steps Evaluate the function at Tap for more steps Replace the variable with in the expression Simplify the result Tap for more steps Simplify each term




Quadratic Function Wikipedia



F X A X H 2 K F X A X H 2 K F X A X H 2 K
01 Reminder For a function of one variable, f(x), we flnd the local maxima/minima by difierenti ation Maxima/minima occur when f0(x) = 0 † x = a is a maximum if f0(a) = 0 and f00(a) < 0;A point where f00(a) = 0 and f000(a) 6= 0 is called a point of in°ection Geometrically, the equation y = f(x) represents a curve in the twoK In this lesson you will learn about graphs of equations of the form y = a ( x − h) 2 k For example, you will look at equations such as y = 3 x 2, y = − 2 x 2, and y = 2 ( x 1) 2 3, and compare them to y = x 2 You will also learn about roots of quadratic equations and how the values of a, h, and k affect the number of roots




2 4 Quadratic Functions Ppt Download




How To Graph A Quadratic Equation 10 Steps With Pictures
Graphing f (x) = a(x − h)2 k The vertex form of a quadratic function is f (x) = a(x − h)2 k, where a ≠ 0 The graph of f (x) = a(x − h)2 k is a translation h units horizontally and k units vertically of the graph of f (x) = ax2 The vertex of the graph of f (x) = a(x − h)2 k is (h, k), and the axis of symmetry is x = h h f(x) = ax2 y x f(x) = a(x − 2h) k k (h, k)Graphing quadratic equations in the form of f(x)=a(xh)^2kExperts are tested by Chegg as specialists in their subject area



Why Is It In Vertex Form Of Quadratic Function Y A X H 2 K Getting Value Of H Is Opposite To Its Value Quora




How To Write Quadratic Functions Video Lesson Transcript Study Com
(a) Find the discriminant of f(x) in terms of k (b) Show that the discriminant of f(x) can be expressed in the form (k a)2 b, where a and b are integers to be found (c) Show that, for all values of k, the equation f(x) = 0 has real roots It's f^prime(g(h(x))) g^prime (h(x)) h^prime(x) Start by defining the function a(x)=g(h(x)) The the chain rule gives us (f @ g @ h)^prime (x)=(f @ alpha)^prime (x)=f^prime(alpha(x)) alpha^prime(x) Applying the definition of alpha(x) to the equation above gives us f^prime(alpha(x)) alpha^prime(x) = f^prime (g(h(x))) (g @h)^prime (x) Using the chain rule again f^prime (g(h(x))) (g @hF(x) = a (x h) 2 k where a, h and k are real numbers with a not equal to zero The first derivative of f is given by f '(x) = 2 a (x h) We analyze the sign of f' using a table f '(x) is positive if a (x h) > 0 We need to consider two cases again and continue solving the inequality above case 1 coefficient a > 0



Vertex And Intercepts




The Graph Of F X X H K Contains The Points 6 2 And 0 2 The Graph Has A Vertex At H 5 Brainly Com
Access Free International Legal English Student S Book With Audio Cds A Course For Classroom Or Self Study Use h—" '—‐"‥‖—‐〃?k 。//googl/JQ8NysHow to Compute the Difference Quotient (f(x h) f(x))/hSo let's put that into this form of the equation f (x) = a (xh)2 k f (x) = a (x−1)2 1 Then we calculate "a" We know the point (0, 15) so f (0) = 15 And a (x−1)2 1 at x=0 is f (0) = a (0−1)2 1 They are both f (0) so make them equal a (0−1)2 1 = 15 Simplify a 1 = 15 a = 05




Graphing Parabolas



Www Scasd Org Cms Lib Pa Centricity Domain 1229 2 2 a2 17 unit 2 2 ws packet lg Pdf




Find The Quadratic Funtion Whose Graph Is Shown To The Right Write The Function In The Form Of F X Brainly Com



Illustrative Mathematics




Quadratic Functions




Quadratic Functions




Ppt Chapter 2 Polynomial Power And Rational Functions Powerpoint Presentation Id




Graphing Quadratics Vertex Form Algebra Video Khan Academy




Section 5 3 Transforming Parabolas Standard Form Vs Vertex Form Standard Form Is Y Ax 2 Bx C Vertex Form Is Y A X H 2 K Ppt Download
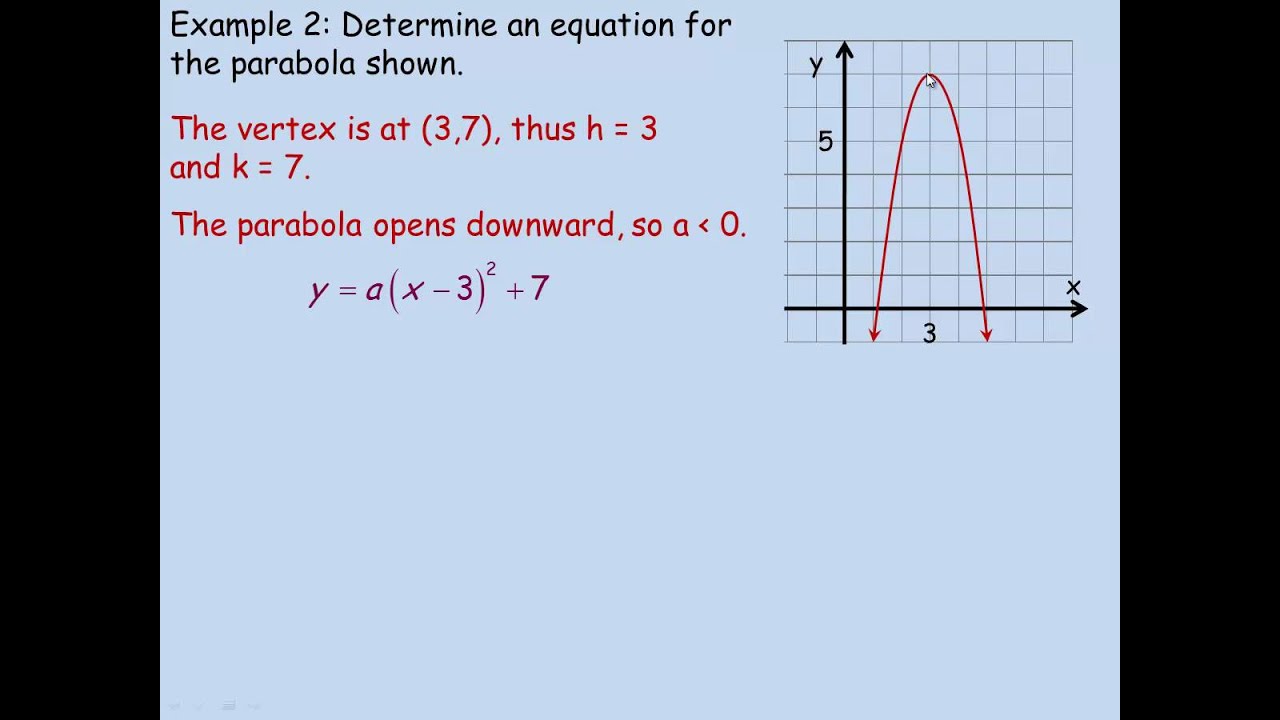



Graphing Y A X H K Youtube




Write The Quadratic Function In The Form F X Chegg Com




Quick Review Before Hw Quiz Y A X H 2 K Form Vertex H K Axis X H Up If A 0 Down If A 0 Ex Y X 1 2 4 Y 1 X 1 2 4 A 1



Assignment 2 Investigating The Relationship Between The Two Standard Forms Of The Graph Of A Parabola
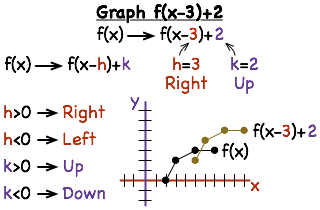



How Do You Graph A Translation Of A Function Printable Summary Virtual Nerd
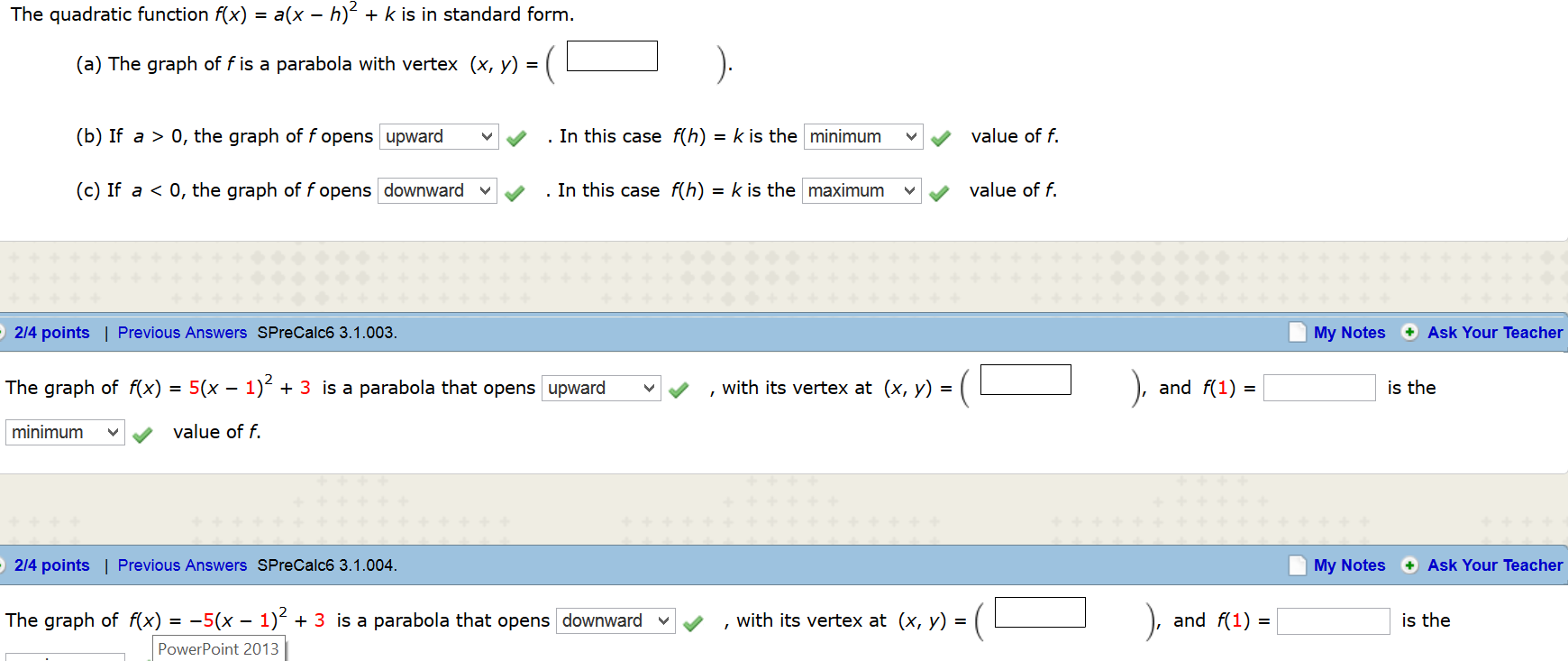



The Quadratic Function F X A X H 2 K Is In Chegg Com




Quadratic Functions
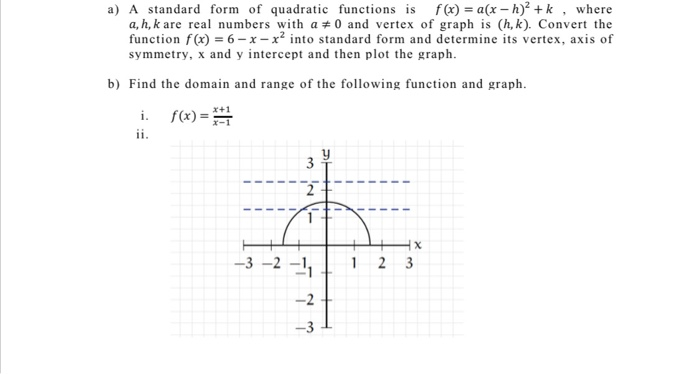



Solved A A Standard Form Of Quadratic Functions Is F X Chegg Com




Identify The Vertex On No 6 Find An Equation Of The Parabola F X U 10 X Homeworklib




Finding Features Of Quadratic Functions Video Khan Academy



Why Is It In Vertex Form Of Quadratic Function Y A X H 2 K Getting Value Of H Is Opposite To Its Value Quora



Polynomial Functions Quadratic Functions Sparknotes




Changing A Quadratic Function Into Vertex Form Youtube



Www Scasd Org Cms Lib Pa Centricity Domain 1229 2 2 a2 17 unit 2 2 ws packet lg Pdf




2 Use The Graph Ofthe Qua Lihat Cara Penyelesaian Di Qanda



Staffweb Psdschools Org Eharding Alg1v Bigideasch 8 A1v8 4notesgraphingf A Xh K Pdf
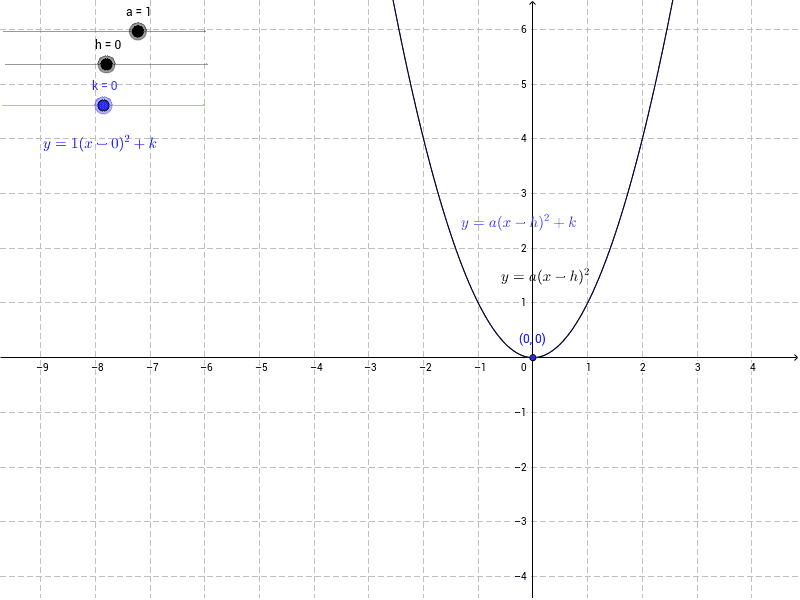



Investigating The Graph Of Y X H 2 K Geogebra




8 4 Graphing F X A X H 2 K Youtube




Vertex Form In 5 Minutes What Is Vertex Form How Do I Find It Mike S Calculators With Steps Free 21
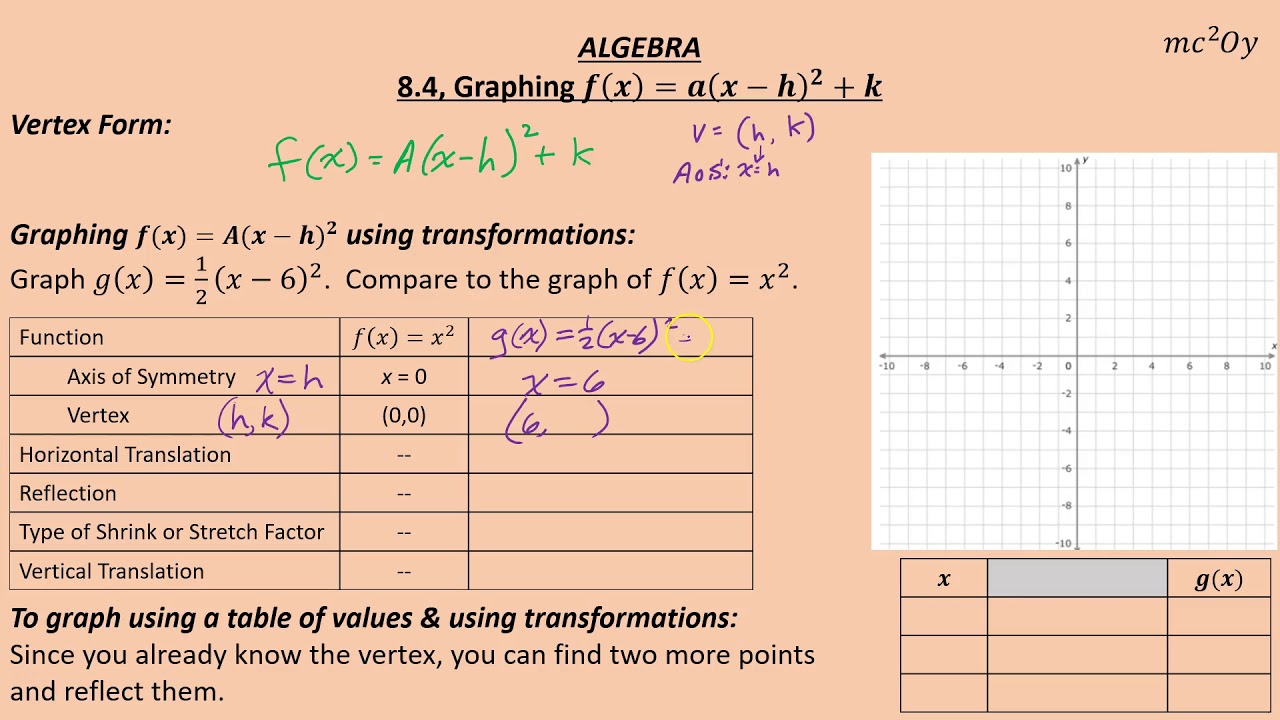



A 8 4 Graphing F X A X H 2 K Youtube



Illustrative Mathematics



Search Q Axis Of Symmetry Tbm Isch
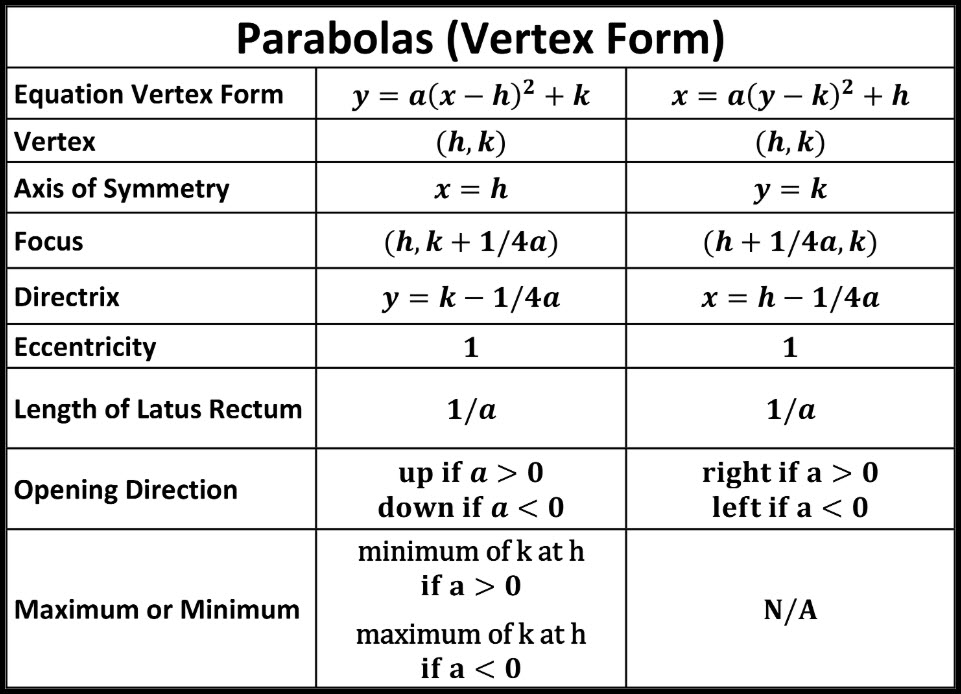



Parabolas Andymath Com



Www Scasd Org Cms Lib Pa Centricity Domain 1229 2 2 a2 17 unit 2 2 ws packet lg Pdf




Quadratic Functions




Quadratic Functions



5 2 Quadratic Functions Mathematics Libretexts
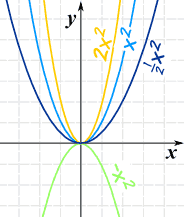



Graphing Quadratic Equations




Quadratic Functions Ppt Download




Vertex Form Introduction Video Khan Academy
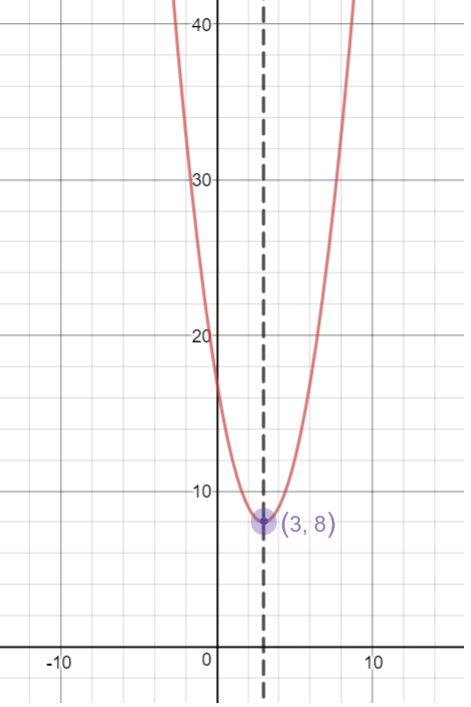



Vertex Form Of A Quadratic Equation Algebra Socratic




Quadratic Function Wikipedia
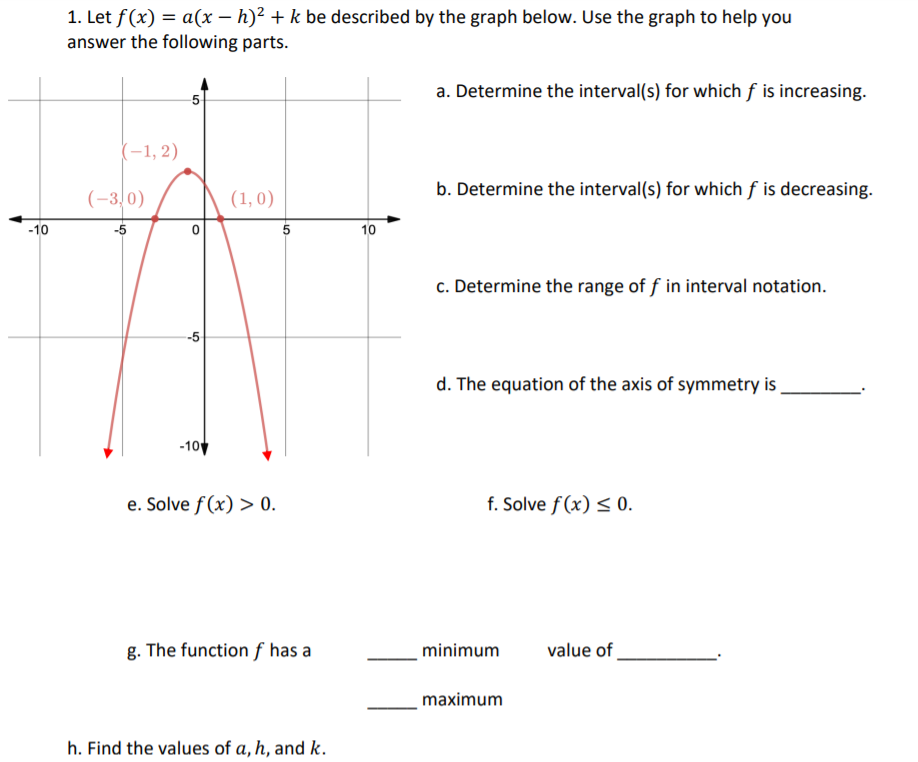



Let F X A X H 2 K Be Described By The Graph Below Chegg Com




Algebra Ii 9 5a Graphs Of F X A X H K Guidelines For Graphing Quadratic Functions Youtube




What Is Vertex Form Example Get Education




How To Graph A Quadratic Equation 10 Steps With Pictures
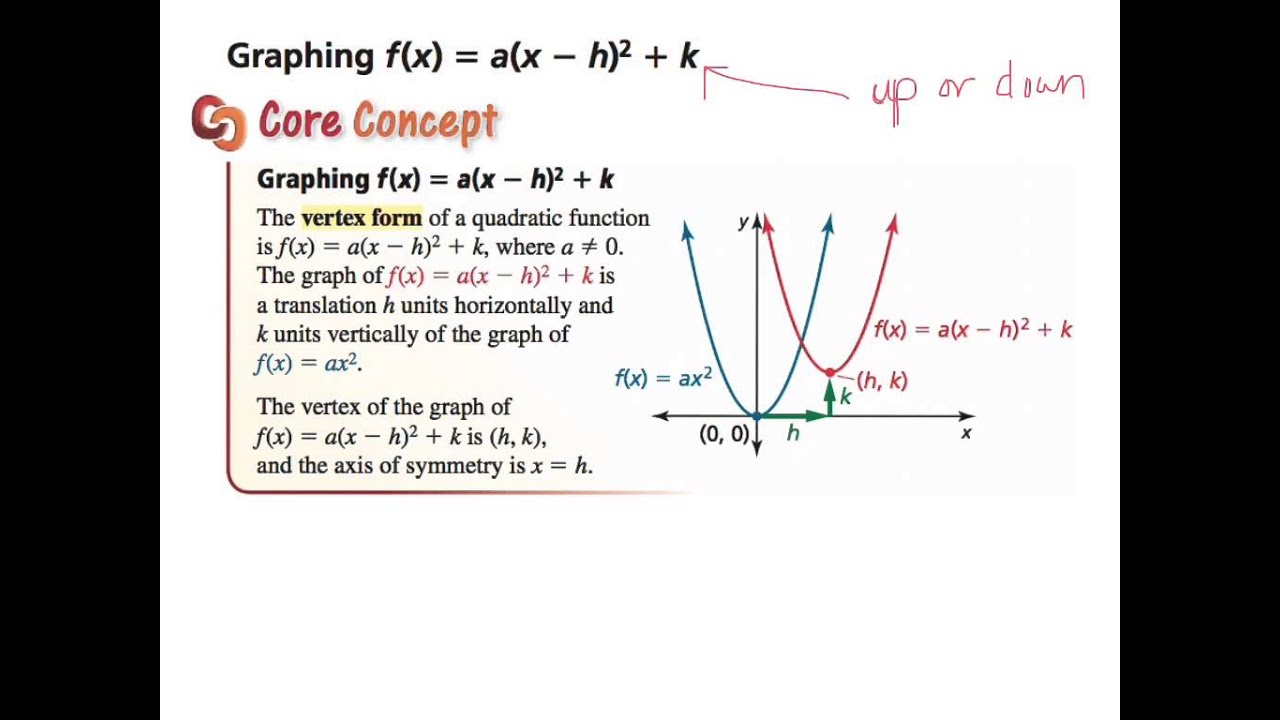



7th Section 8 4 Graphing F X A X H 2 K Youtube



1



Quadratic Function
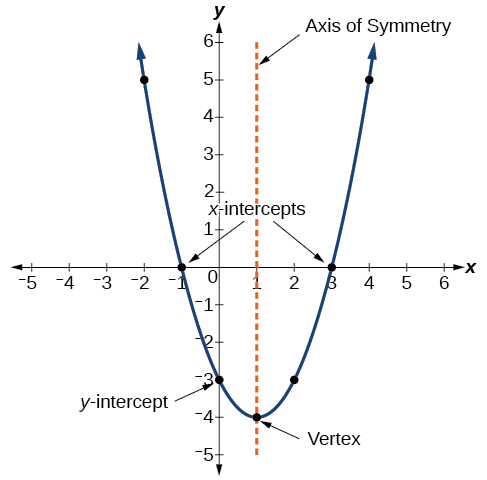



5 2 Quadratic Functions Mathematics Libretexts




Quadratic Functions
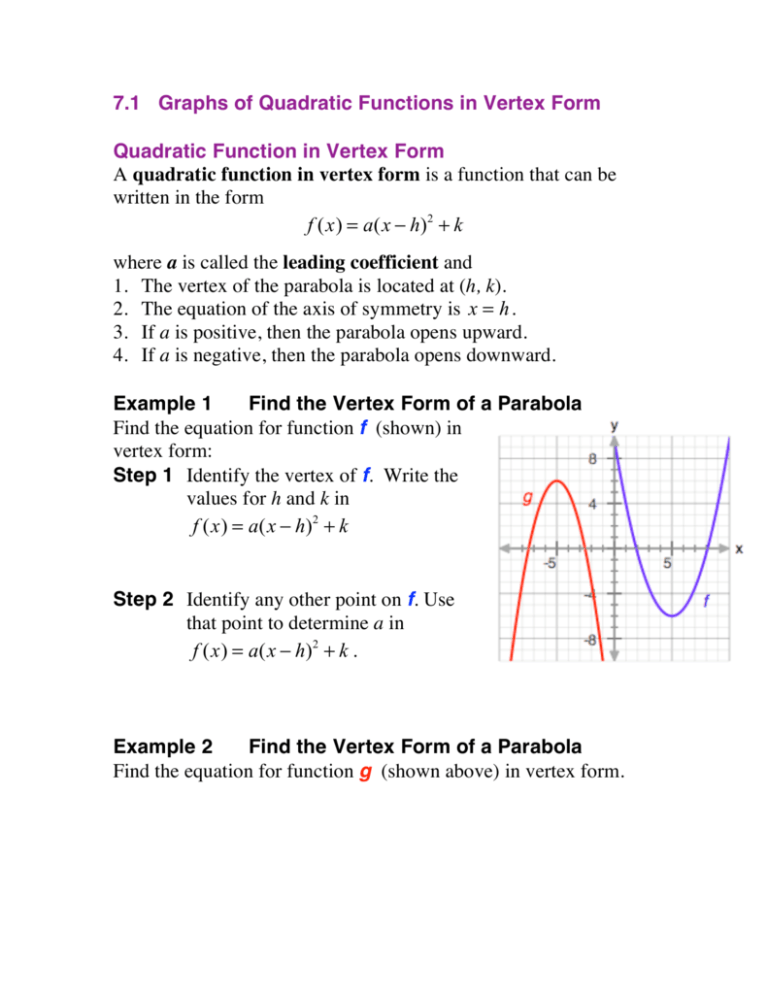



F X A X H 2 K F X A X H 2 K F X A X H 2 K




3 Ways To Find The Inverse Of A Quadratic Function Wikihow




Ex Write Ax 2 Bx C In The Form A X H 2 K Negative A Youtube
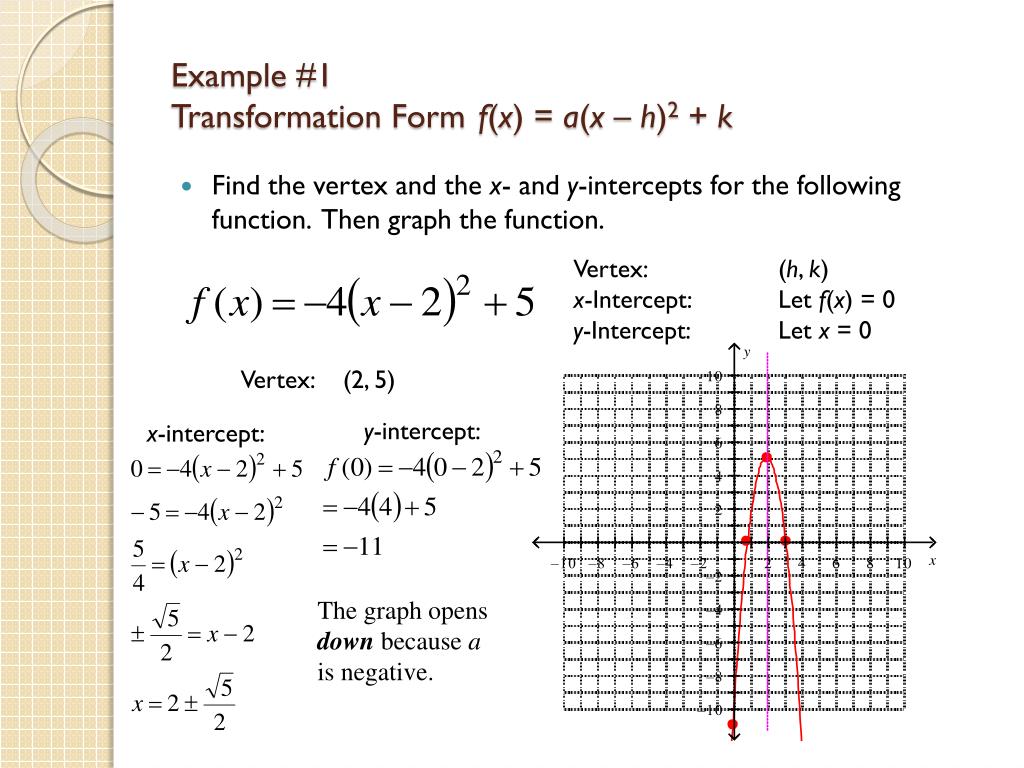



Ppt 3 3 Quadratic Functions Powerpoint Presentation Free Download Id




Transformations Review Vertex Form Y A X H 2 K The Vertex Form Of A Quadratic Equation Allows You To Immediately Identify The Vertex Of A Parabola Ppt Download




Graphing Parabolas




Quadratic Function Wikipedia



Solved Use The Graph Of The Quadratic Function F X A X H 2 K To Find The Vertex Axis Of Symmetry And The Minimum Or Maximum Value Of The Functi Course Hero



Illustrative Mathematics
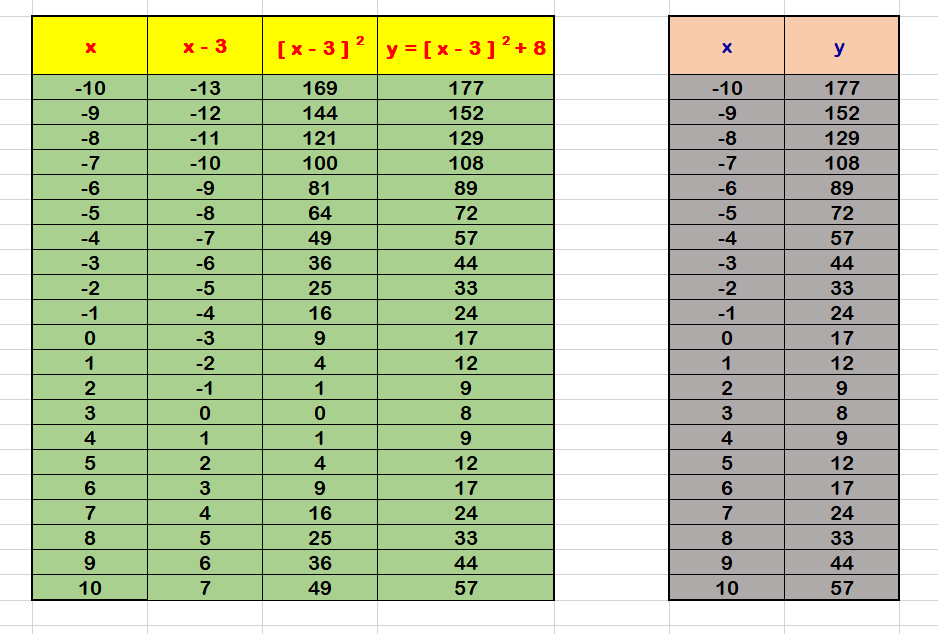



Vertex Form Of A Quadratic Equation Algebra Socratic
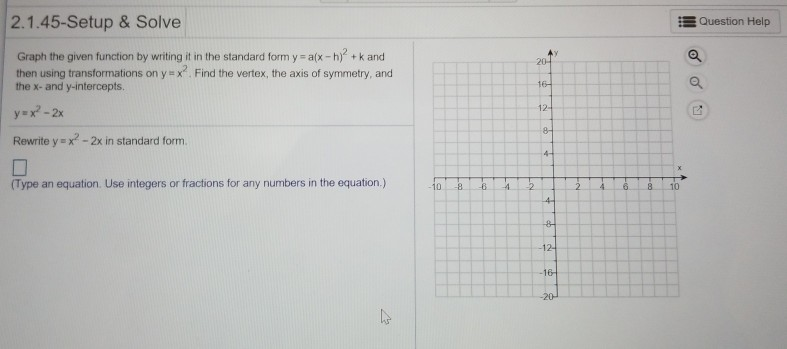



For The Following Problem Find The Quadratic Chegg Com



Solution Write The Quadratic Function In The Form F X A X H 2 K Find The Vertex And Graph The Function A F X X 2 6x B F X X 2 4x 1 C F X 3x 2 10x 2




Ex Write Ax 2 Bx C In The Form A X H 2 K Negative A Youtube




Quadratic Functions Ppt Download




Quadratic Functions In Vertex Form Ppt Download
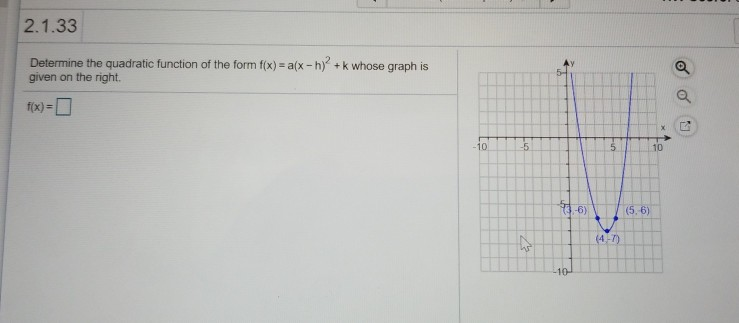



For The Following Problem Find The Quadratic Chegg Com



1




I Need To Write The Given Function In The Form Of Chegg Com




Calgebra A1 8 4 Graphing F X A X H 2 K Youtube




Handout Or Power Point Presentation To Accompany Lesson




Graphing Parabolas
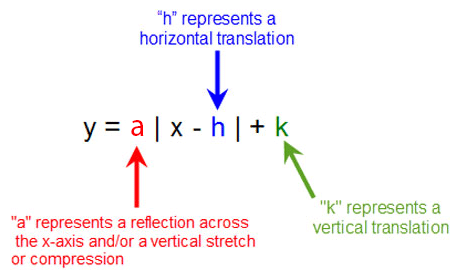



Transformations Of Absolute Value Functions Texas Gateway
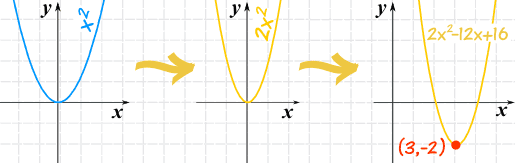



Graphing Quadratic Equations
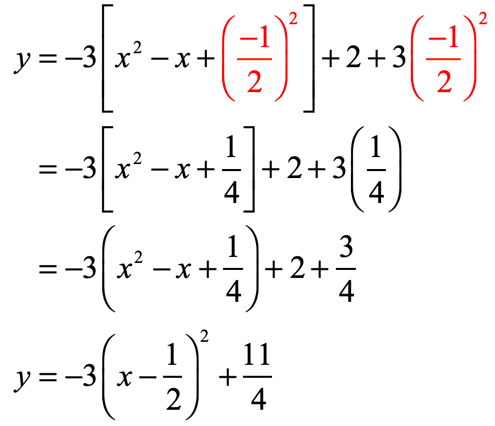



Completing The Square Step By Step Chilimath
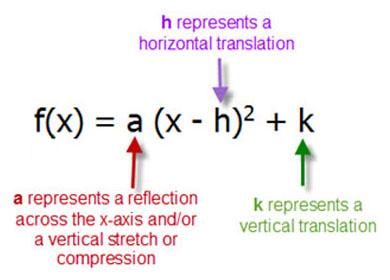



Untitled Document
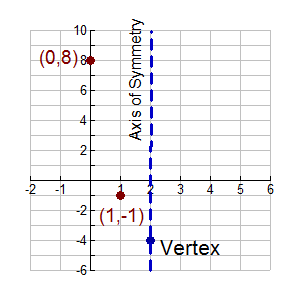



Vertex Form Of Quadratic Equation Mathbitsnotebook A1 Ccss Math



Solved Use The Vertex H K And The Point On The Graph Xy To Find The Standard Form F X A X H 2 K Of This Equation Quadratic Function Course Hero
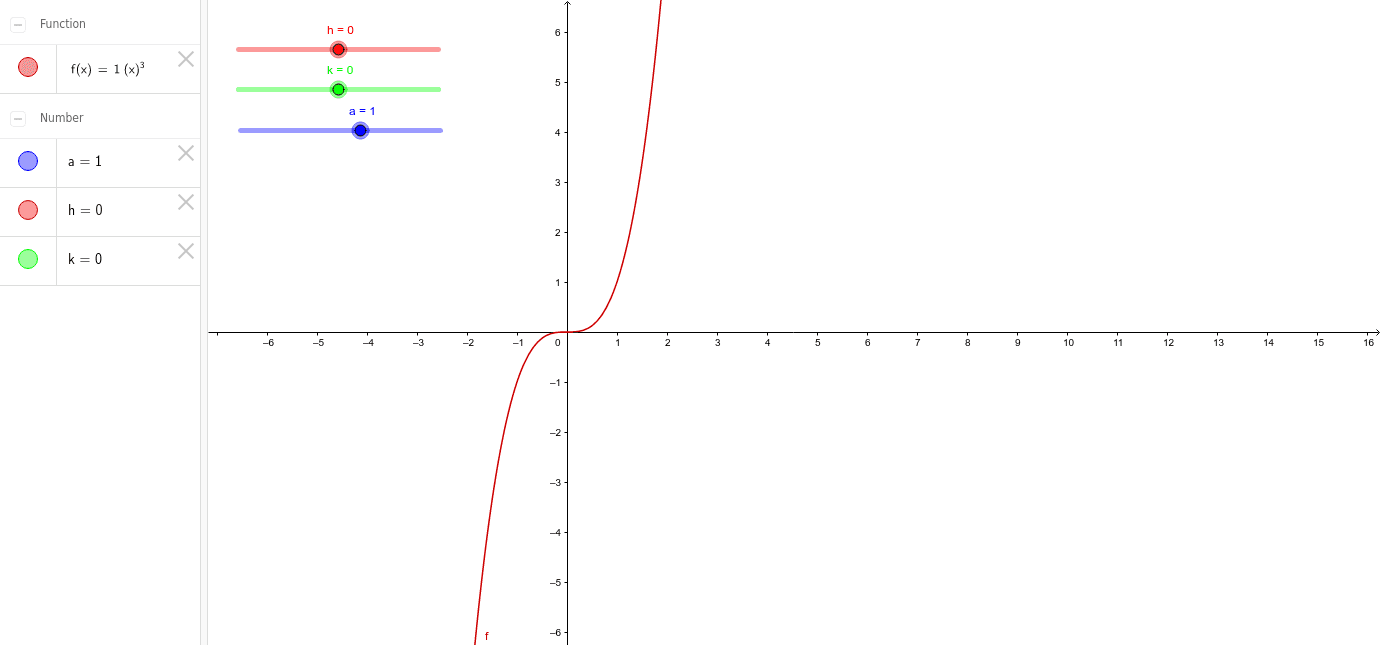



Y A X H 3 K Geogebra



0 件のコメント:
コメントを投稿